Hardy-Weinberg-Gesetz
nach dem englischen Mathematiker Godfrey Harold Hardy (1877 - 1947) und dem deutschen Arzt Wilhelm Weinberg (1862 - 1937)
Synonyme: Hardy-Weinberg-Gleichgewicht, HWG
Englisch: Hardy-Weinberg principle
Definition
Das Hardy-Weinberg-Gesetz ist ein mathematisches Modell aus der Populationsgenetik. Es ermöglicht die Bestimmung der Häufigkeiten dominant-rezessiv vererbter Genotypen beim diploiden Chromosomensatz.
Hintergrund
Das Hardy-Weinberg-Gesetz findet hauptsächlich in der klinischen Genetik Gebrauch, um die Heterozygotenhäufigkeit bei autosomal-rezessiv vererbten Krankheiten zu bestimmen, insofern nur die Krankheitshäufigkeit bekannt ist.
Das Gesetz geht davon aus, dass an einem ganz bestimmten Genlocus zwei unterschiedliche Allele vorliegen. Diese kennzeichnet man üblicherweise mit "p" und "q" - z.B. ein Normalallel (traditionell p) und ein Krankheitsallel (traditionell q). Da nur diese beiden Allele vorkommen, ist deren Summe p + q = 1. Liegt somit das entsprechende Gen beim Menschen nun auf einem Autosom in zwei Kopien vor, so ergibt sich die Häufigkeit der drei möglichen Genotypen aus der Binominalbeziehung:
- (p + q)2 = pp + pq + qp + qq = p2 + 2pq + q2 = 1
Die Formel lässt sich bildlich gut als Quadratfläche darstellen. Hier stehen die Seitenflächen jeweils für ein Chromosom (mit den spezifischen Wahrscheinlichkeiten der jeweiligen Allele p und q).
Bei seltenen rezessiven Krankheiten kommt das krankheitsauslösende Allel sehr viel seltener vor als das Normalallel. q ist nahe 0 und p nahe 1, q2 also sehr viel kleiner als p2. Die Heterozygotenhäufigkeit 2pq hängt v.a. vom Wert für q ab. Im selben Zug kann p mit 1 gleich gesetzt werden. Um eine Heterozygotenhäufigkeit in einer Population bestimmen zu können, muss man die Wurzel der Häufigkeit einer rezessiven Krankheit ziehen und mit 2 multiplizieren. Tritt beispielsweise eine Krankheit mit einer Inzidenz von q2 = 1:40.000 auf, ist die theoretische Überträgerfrequenz 2 · (1:200) = (1:100) = 1%.
Berechnung
Wenn an einem Genort zwei Allele existieren, die als p und q bezeichnet wurden, gilt für die Allelfrequenz:
Die Häufigkeit der drei möglichen Genotypen AA, Aa und aa ergibt sich aus der Binominalbeziehung:
Für autosomal-rezessive Krankheiten, bei denen das krankheitsauslösende Allel q sehr viel seltener vorkommt als das normale Allel p, ergibt sich:
Beispiel
In der klinischen Praxis kann es manchmal sinnvoll sein, das Bayes-Theorem und das Hardy-Weinberg-Gesetz gemeinsam anzuwenden. Folgendes Beispiel illustriert diese Situation:
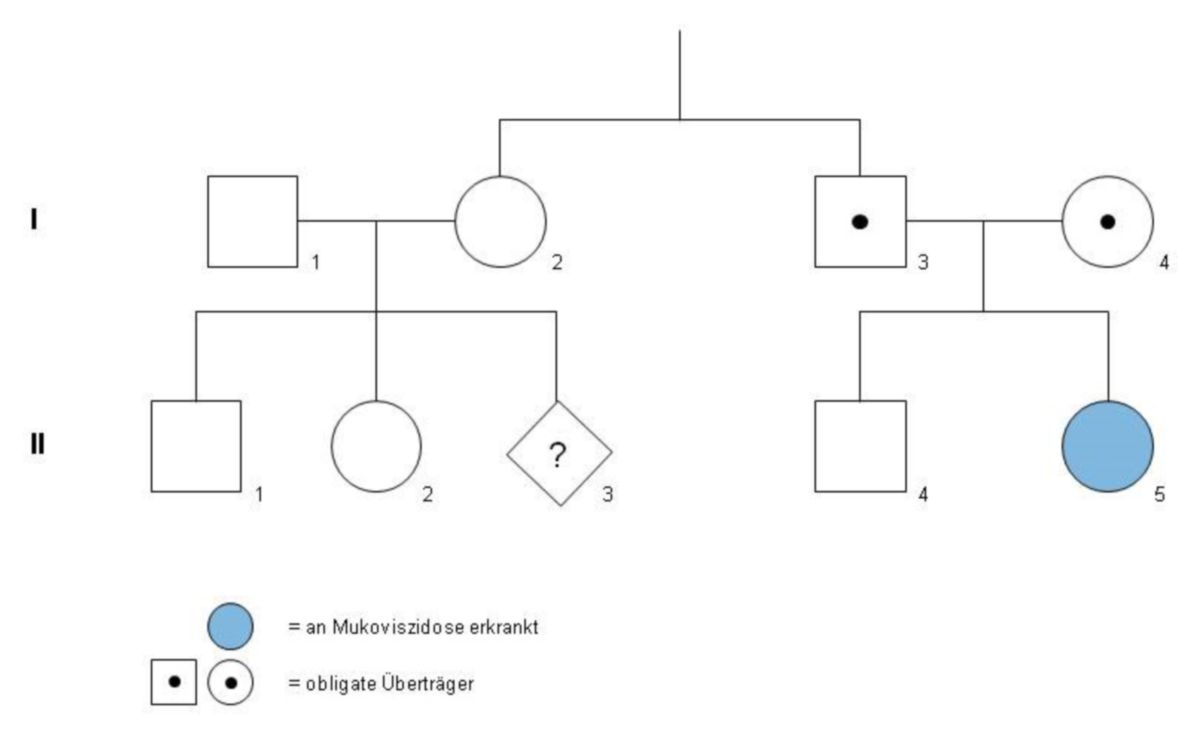
Herr Maier und seine Frau (I1 und I2) haben zusammen zwei gesunde Kinder. Vor kurzer Zeit jedoch bekamen sie die Information, dass eine Nichte von Frau Maier an Mukoviszidose erkrankt ist. Sie möchte aufgrund dessen nachfragen, wie hoch das Risiko für Mukoviszidose bei einem dritten gemeinsamen Kind ist.
- 1. Frage: Wie hoch ist die Wahrscheinlichkeit, dass Frau Maier Überträgerin für Mukoviszidose ist? Mit Sicherheit ist einer ihrer Eltern Überträger(in), weshalb sie selbst mit einer Wahrscheinlichkeit von 50% (½) Überträgerin einer Mukoviszidosemutation ist.
| Bayes-Theorem | ||
|---|---|---|
| I1 und I2 sind beide Carrier | I1 und I2 sind nicht beide Carrier | |
| a-priori-Wahrscheinlichkeit | ½ · 1/25 = 1/50 | 1 - 1/50 = 49/50 |
| bedingte Wahrscheinlichkeit (zwei gesunde Kinder) | (3/4)2 = 9/16 | 1 |
| kombinierte Wahrscheinlichkeit | 9/800 | 49/50 = 748/800 |
| a-posteriori-Wahrscheinlichkeit | 9/800 ÷ 793/800 = 9/793 ≈ 1/88 | 748/800 ÷ 793/800 = 784/793 ≈ 87/88 |
- 2. Frage: Wie hoch ist die Wahrscheinlichkeit, dass Herr Maier Überträger für Mukoviszidose ist? Herr Maier hat keine bekannten Verwandten mit der Erkrankung. Für ihn gilt somit das Bevölkerungsrisiko, das sich mit der Hardy-Weinberg-Formel berechnen lässt. Die Mukoviszidose-Inzidenz in der Bevölkerung (q2) beträgt 1/2.500. Man kann daraus die Allelfrequenz q als √1/2.500 = 1/50 und die Heterozygotenfrequenz (2 · 1/50) als ca. 1/25 bzw. 4% berechnen.
- 3. Frage: Wie groß ist die Wahrscheinlichkeit für ein betroffenes Kind, wenn man die gesunden Kinder nicht berücksichtigt? Die Wahrscheinlichkeit, dass beide Eheleute Überträger sind, liegt bei 1/50 (½ · 1/25) bzw. 2%. Hier besteht also ein Risiko von ¼ für ein betroffenes Kind. Das Gesamtrisiko beträgt somit 1/50 · ¼ = 1/200 (0,5%).
- 4. Frage: Wie hoch ist die Wahrscheinlichkeit für ein betroffenes Kind, wenn man die gesunden Kinder berücksichtigt? Wie man der Tabelle oben entnehmen kann, reduziert sich die Wahrscheinlichkeit - dass beide Eltern (Maier) Überträger sind - auf 1/88. Das Erkrankungsrisiko für ein Kind reduziert sich dementsprechend auf ca. 1/350 (0,3%).
Störfaktoren
Das Hardy-Weinberg-Gesetz findet nur bei "idealen Populationen" Anwendung - somit müssen folgende Voraussetzungen erfüllt sein:
- Paarungen müssen innerhalb einer Population zufällig erfolgen und mit gleicher Wahrscheinlichkeit und gleichem Erfolg für die unterschiedlichen Genotypen (Panmixie).
- Die Population muss so groß sein, dass zufällige Ereignisse (Gendrift) keinen relevanten Einfluss auf die Allelfrequenz haben können.
- Es darf kein Selektionsvorteil oder gar Selektionsnachteil für die Träger bestimmter Genotypen bestehen.
- Es herrschen keine Neumutationen vor.
- Es darf keine Zu- oder Abwanderung stattfinden (Migration), die die Allelfrequenz womöglich verändern könnte.
Vor allem die Panmixie ist von all diesen Voraussetzungen von praktischer Bedeutung. Grund dafür ist, dass das Hardy-Weinberg-Gesetz nicht angewendet werden kann, wenn Verwandtenehen häufig sind. Konsanguinität darf somit nicht vorherrschen. In einem solchen Fall kommen seltene rezessive Krankheiten sehr viel häufiger vor, als sich aus der Heterozygotenfrequenz ableiten ließe. Die anderen vier Voraussetzungen sind eher für die Frage wichtig, ob Allel- oder Genotypfrequenzen über die Zeit konstant bleiben oder ob sich die Häufigkeit einer Krankheit verändert.
Literatur
- "Basiswissen Humangenetik" - Christian P. Schaaf, Johannes Zschocke, Springer-Verlag