Genetisches Risiko
Synonyme: Genetische Risikowahrscheinlichkeit
Englisch: genetic risk score
Definition
Das genetische Risiko ist einer der wichtigsten Aspekte einer genetischen Beratung. Es drückt die Wiederholungs- bzw. Vererbungswahrscheinlichkeit einer Mutation bzw. einer Erbkrankheit aus. Grundlage des genetischen Risikos ist der Erbgang, zusätzlich werden Penetranz, Neumutationsrate und Allelfrequenzen berücksichtigt.
Berechnungsgrundlagen
Additionssatz
Zwei Ereignisse, A und B, schließen sich wechselseitig aus und können somit nicht gleichzeitig eintreten. Diese beiden Ereignisse nennt man somit unvereinbar. Liegt aber die Wahrscheinlichkeit vor, dass Ereignis A eintritt bei P(A) und die Wahrscheinlichkeit, dass Ereignis B eintritt bei P(B), kann man draus schließen, dass die Wahrscheinlichkeit P(A∪B), dass entweder Ereignis A oder Ereignis B eintritt, P(A) + P(B) entspricht.
- Beispiel: Zwillinge können entweder eineiig oder zweieiig sein. Die Wahrscheinlichkeit für ein eineiiges Zwillingspaar (EZ) liegt bei P(EZ) = ⅓. Die Wahrscheinlichkeit, dass ein zweieiiges Zwillingspaar (ZZ) entsteht, liegt bei P(ZZ) = ⅔. Wendet man hier also den Additionssatz an, so liegt die Wahrscheinlichkeit dafür, dass das Zwillingspaar entweder eineiig oder zweieiig ist, bei P(EZ∪ZZ) = ⅓ + ⅔ = 1. Kurz gesagt: Die Summe aller Möglichkeiten (EZ, ZZ) ist 1.
Multiplikationssatz
Sind zwei Ergebnisse, A und B, voneinander unabhängig, tritt der Multiplikationssatz in Kraft. Für die Wahrscheinlichkeit, dass sowohl A als auch B eintreten gilt:
Beispiel 1
Die Wahrscheinlichkeit, dass eine Fehlgeburt eintritt, ist (bei Fehlen besonderer Riskikofaktoren) etwa 1/6. Dieselbige Zahl gilt auch für Schwangerschaften derjenigen Paare, die schon in der ersten Schwangerschaft eine Fehlgeburt hatten. Man kann also daraus die Wahrscheinlichkeit berechnen: (P∩B) von 1/6 · 1/6 = 1/36, anders ausgedrückt auch als 3% (≈ 0,027). Diese Zahl erklärt, wieso bei der Mehrheit der Paare mit ungeklärten Fehlgeburten keine Riskikofaktoren vorliegen und somit nachfolgende Schwangerschaften normal ausgetragen werden können.
Beispiel 2
Dieses Beispiel handelt vom Zusammentreffen von zwei unterschiedlichen Krankheitsbildern beim gleichen Patienten. Die Wahrscheinlichkeit, dass bei einer Frau im Laufe ihres Lebens (Lebenszeitwahrscheinlichkeit) Brustkrebs auftritt, liegt in etwa bei 8% (0,08). Hiervon sind in etwa 5% der Brustkrebsfälle auf familiäre Krebserkrankungen zurückzuführen. Die selbige Wahrscheinlichkeit - jedoch für Eierstockkrebs (Lebenszeitwahrscheinlichkeit) liegt in der Normalbevölkerung ca. bei 1%. Frauen, die eine familiäre Prädisposition vorweisen können, haben eine Wahrscheinlichkeit von 50%, im Laufe ihres Lebens an Eierstockkrebs zu erkranken.
Man schätzt die Prävalenz von Mutationen in einem der beiden Brustkrebsgene BRCA1 bzw. BRCA2 bei Frauen in etwa auf 0,5% (1:200 bzw. 0,005). Tritt nun bei einer Frau sowohl Brust- als auch Eierstockkrebs auf, so liegt die Wahrscheinlichkeit, dass keine Krebsdisposition vorliegt (also beide Erkrankungen treten völlig unabhängig voneinander auf) - bei 0,08 · 0,01 - also 0,0008 bzw. 1:1.250. Um die Wahrscheinlichkeit - dass das Zusammentreffen der beiden Krebsarten auf eine familiäre Krebsdisposition zurückzuführen ist - zu errechnen, verwendet man dagegen 0,05 · 0,8 · 0,5 = 0,002 bzw. 1:500. Die Wahrscheinlichkeit für eine zugrundeliegende Krebsdispositon ist mehr als doppelt so hoch wie das zufällige Zusammentreffen der beiden Krebsarten. Jedoch sind beide Varianten möglich - und treten somit in der Natur auf.
Bayes-Theorem
Das 1763 von Thomas Bayes publizierte Bayes-Theorem ist heute noch die wichtigste Methode zur Berechnung tatsächlicher Erkrankungswahrscheinlichkeiten in der klinischen Genetik und in der Medizin im Allgemeinen. Diesem Theorem kommt zugute, dass es bei der Berechnung einer Wahrscheinlichkeit zusätzliche Informationen (die ggf. leicht zu ermitteln sind) mit einfließen lässt.
Das von Bayes erstellte Theorem enthält drei wesentliche Schritte:
- Festlegung einer A-priori-Wahrscheinlichkeit
- Einbeziehen zusätzlicher Informationen
- Berechnung einer A-posteriori-Wahrscheinlichkeit
| Risikoberechnung (Bayes-Theorem) | ||
|---|---|---|
| Ereignis/Möglichkeit A | Ereignis/Möglichkeit B | |
| A-priori-Wahrscheinlichkeit (a+b=1) | a (oder 1-b) | b (oder 1-a) |
| Bedingte Wahrscheinlichkeit | c | d |
| Kombinierte Wahrscheinlichkeit | ac | bd |
| A-posteriori-Wahrscheinlichkeit | ac÷(ac+bd) | bd÷(ac+bd) |
Beispiel 1
Die a-priori-Wahrscheinlichkeit für die Tochter einer gesicherten Überträgerin der Krankheit Muskeldystrophie Duchenne liegt bei 50% (0,5). Bezieht man jedoch zusätzliche Informationen ein, wie z.B. durch die Bestimmung des CK-Wertes, so können die Vorabwahrscheinlichkeiten modifiziert werden. Dazu muss man die bedingte Wahrscheinlichkeit berechnen, mit der bei beiden Szenarien ein bestimmter Befund erhoben wird. Dazu zählt eben z.B. mit welcher Wahrscheinlichkeit die CK-Werte bei einer Überträgerin bzw. bei einer Normalperson (Frauen: <145 U/l) erhöht oder eben nicht erhöht sind. In unserem Fall nehmen wir an, dass 70% aller Überträgerinnen erhöhte CK-Werte aufweisen. Im Gegenzug weisen nur 5% der Normalpersonen (keine Überträger) eine Erhöhung derselben Werte auf. Um die kombinierte Wahrscheinlichkeit aus der a priori Wahrscheinlichkeit und bedingt Wahrscheinlichkeit ausrechen zu können, muss man den Multiplikationssatz anwenden (Abbildung unten).
Bei der Aufstellung dieser Rechnung ergibt sich eine Vier-Felder-Tafel, in der alle vier Möglichkeiten dargestellt werden. Um eine weitere Berechnung anstellen zu können, lässt man die beiden Felder wegfallen, die nicht in Frage kommen. Anschließend werden die Wahrscheinlichkeitsziffern der beiden verbleibenden Felder zusammengezählt und als neue Referenzgröße verwendet (in unserem Beispiel wäre dies 0,375 für den Fall, dass die Creatinkinasewerte erhöht sind). Somit erhält man schlussendlich die a-posteriori-Wahrscheinlichkeit, also die Wahrscheinlichkeit, die das ursprüngliche Szenario und zusätzlich noch die hinzukommenden Informationen in einer einzigen Risikoziffer vereint. Diese ergibt sich aus dem Anteil der kombinierten Wahrscheinlichkeit an dieser Referenzgröße (hier: 0,933 für einen Überträgerstatus - 0,067 für eine Normalperson) - das heißt, dass die Frau mit erhöhten CK-Werten mit einer Wahrscheinlichkeit von 93% Überträgerin ist.
Beispiel 2
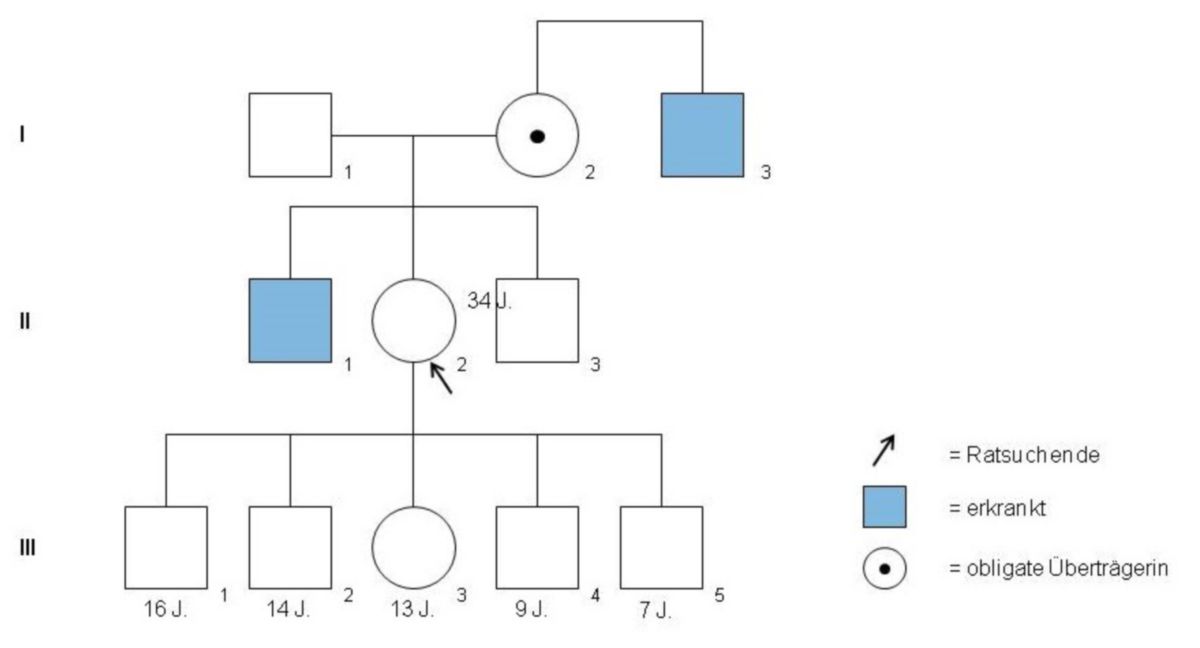
Anhand eines zweiten Beispiels soll die Wahrscheinlichkeitsberechnung nach Bayes zur Muskeldystrophie Duchenne nochmals erläutert werden: Eine Ratsuchende sucht abermals eine genetische Beratungsstelle auf, da sie wissen will, ob sie eine Überträgerin ist. Grundlage ihrer Nachfrage ist, dass sie die Tochter einer obligaten Überträgerin ist, da sowohl ihr Onkel mütterlicherseits, als auch der Bruder an derselbigen Muskeldystrophieform erkrankt waren. Dank dieser Vorabinformation kann eine Berechnung der A-priori-Wahrscheinlichkeit für Situation A (Carrier) und Situation B (kein Carrier) erfolgen. Beide liegen jeweils bei ½. Außerdem schließen sich beide Ergebnisse wechselseitig aus und ihre Summe beträgt 1 (0,5 + 0,5).
Nun kommt eine weitere Information hinzu: die Ratsuchende hat bereits vier Söhne. Alle sind gesund. Es lässt sich errechnen, dass die bedingte Wahrscheinlichkeit, dass alle vier Söhne einer Überträgerin gesund sind, bei (½)4 = 1/16 liegt (aus der anderen Sichtweise: mit der Wahrscheinlichkeit von 15/16 wäre mindestens ein Sohn erkrankt). Auch hier findet erneut der Multiplikationssatz Anwendung, denn die einzelnen Schwangerschaften stellen voneinander unabhängige Ereignisse dar. Falls sich herausstellt, dass B keine Überträgerin für die Muskeldystrophie ist, kann sie also auch nur gesunde Söhne bekommen und die bedingte Wahrscheinlichkeit liegt somit bei 1.
Man bringt alle diese Informationen (entsprechend der unten folgenden Tabelle) in die Berechnung mit ein. Es resultiert eine A-posteriori-Wahrscheinlichkeit für Situation A, dass B Überträgerin ist, von 1/17 und eine A-posteriori-Wahrscheinlichkeit dafür, dass sie keine Überträgerin ist, von 16/17. Man kann an diesem Beispiel erkennen, wie erheblich sich die Risikoziffer ändert, wenn alle relevanten Informationen berücksichtigt werden.
| Wahrscheinlichkeitsberechnung | ||
|---|---|---|
| B ist Carrier | B ist kein Carrier | |
| a-priori-Wahrscheinlichkeit | ½ | ½ |
| bedingte Wahrscheinlichkeit | (½)4 = 1/16 | 1 |
| kombinierte Wahrscheinlichkeit | ½ · 1/16 = 1/32 | ½ · 1 = ½ = 16/32 |
| neuer Referenzwert = 17/32 | ||
| a-posteriori-Wahrscheinlichkeit | 1/32 ÷ 17/32 = 1/17 | 16/32 ÷ 17/32 = 16/17 |
Literatur
- "Basiswissen Humangenetik" - Christian P. Schaaf, Johannes Zschocke, Springer-Verlag