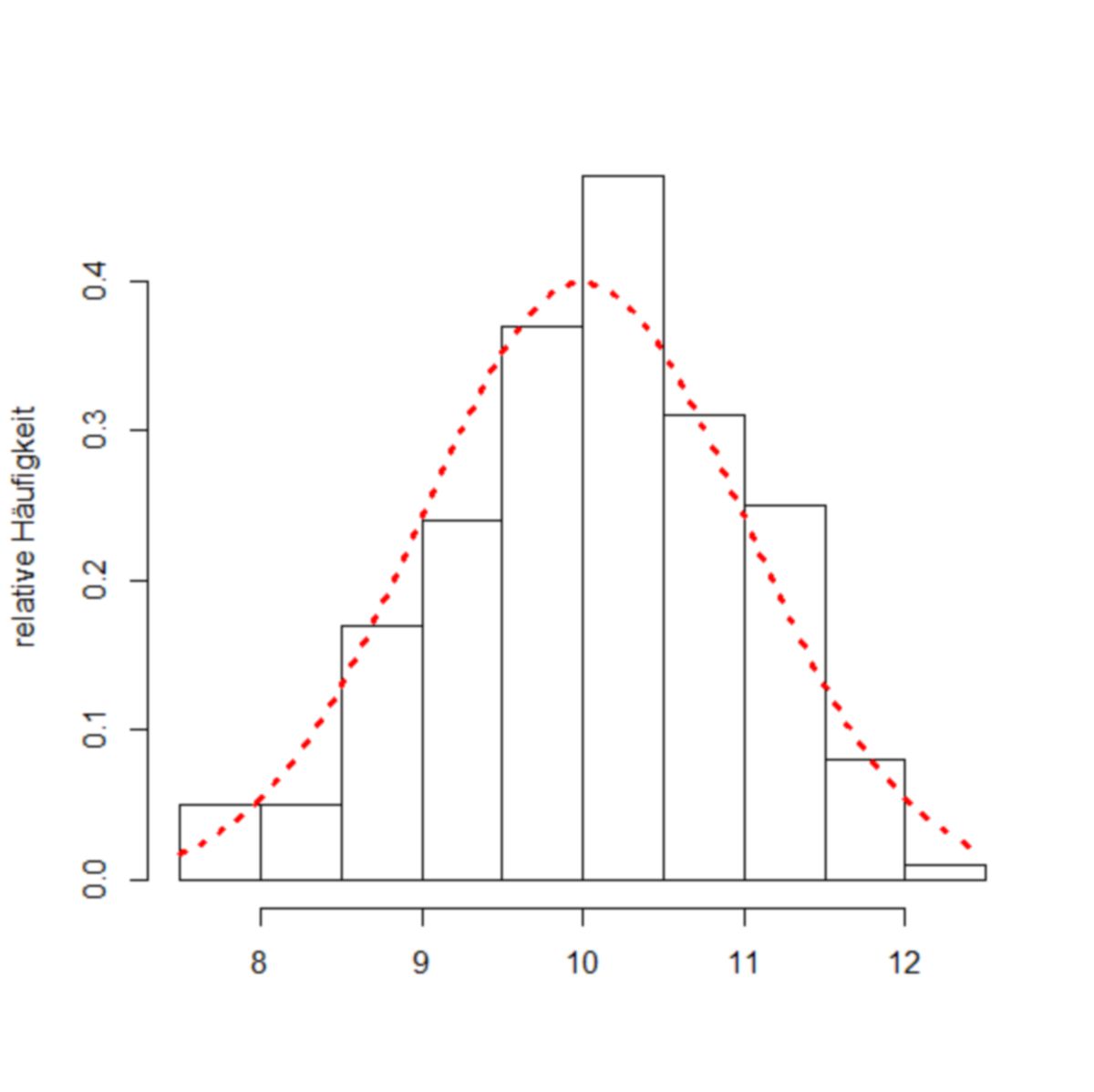
Normalverteilung

Die Normalverteilung bezeichnet eine wichtige Form der Wahrscheinlichkeitsverteilung. Man bezeichnet die graphische Auftragung ihrer Dichtefunktion auch als Glockenkurve oder Gauß-Kurve. Ihr Kurvenverlauf ist symmetrisch, wobei Modalwert, Median und arithmetischer Mittelwert identisch sind.

Die Normalverteilung findet in der Statistik häufig Anwendung bei großen Grundgesamtheiten. Die Bedeutung der Normalverteilung ergibt sich aus dem Umstand, dass Verteilungen, die durch Überlagerung vieler kleiner Effekte entstehen, bei ausreichend großer Stichprobenzahl näherungsweise einer Normalverteilung entsprechen ("Zentraler Grenzwertsatz"). Daher lassen sich viele natürliche, komplexe Phänomene durch eine Normalverteilung beschreiben. Zufallsgrößen mit Normalverteilung benutzt man zur Beschreibung zufälliger Vorgänge wie z. B. Messfehler.

Die Normalverteilung der Daten ist meist eine Voraussetzung für die Durchführung parametrischer Tests, wie des t-Tests. Biologische Parameter wie z.B. Protein- und mRNA-Expressionslevel sind oft log-normalverteilt, das bedeutet sie müssen zunächst mit einem Logarithmus transformiert werden, um einer Normalverteilung zu entsprechen.

Eine Sonderform der Normalverteilung ist die Standardnormalverteilung. Sie hat einen Mittelwert (Erwartungswert) von 0 und eine Varianz von 1. Jede Normalverteilung kann durch geeignete Transformation in eine Standardnormalverteilung umgerechnet werden.

Die Grafik zeigt ein Histogramm einer Stichprobe der Größe 200 mit einem Mittelwert von 10 und einer Standardabweichung von 1, überlagert mit der Dichtefunktion einer Normalverteilung mit den gleichen Parametern (gestrichelte rote Linie).

Ein bekanntes Beispiel eine Normalverteilung in der Medizin ist die Price-Jones-Kurve, die Häufigkeitsverteilung der Erythrozytengröße. Der Mittelwert dieser Verteilung ist das MCV.