Kabel-Theorie

Die Kabel-Theorie ist eine mathematische Theorie zur Berechnung der passiven Erregungsleitung entlang von Nervenzellfortsätzen.

Die Kabel-Theorie basiert auf einer von William Thompson in den 1850er Jahren entwickelten Theorie zur Beschreibung des Abklingens von Signalen bei Unterwassertelegrafenkabeln. Hodgkin und Rushton modifizierten diese Theorie 1946 und bezogen sie auf die passive Erregungsleitung in Nervenzellen.^[1]

Eine passive Erregungsleitung kommt beim Menschen nur in einigen Dendriten vor. Die aktive Erregungsleitung, z.B. in Axonen, ist nicht Teil der Kabel-Theorie, da hierfür zusätzlich die spannungsgesteuerten Na⁺- und K⁺-Kanäle berücksichtigt werden müssten.

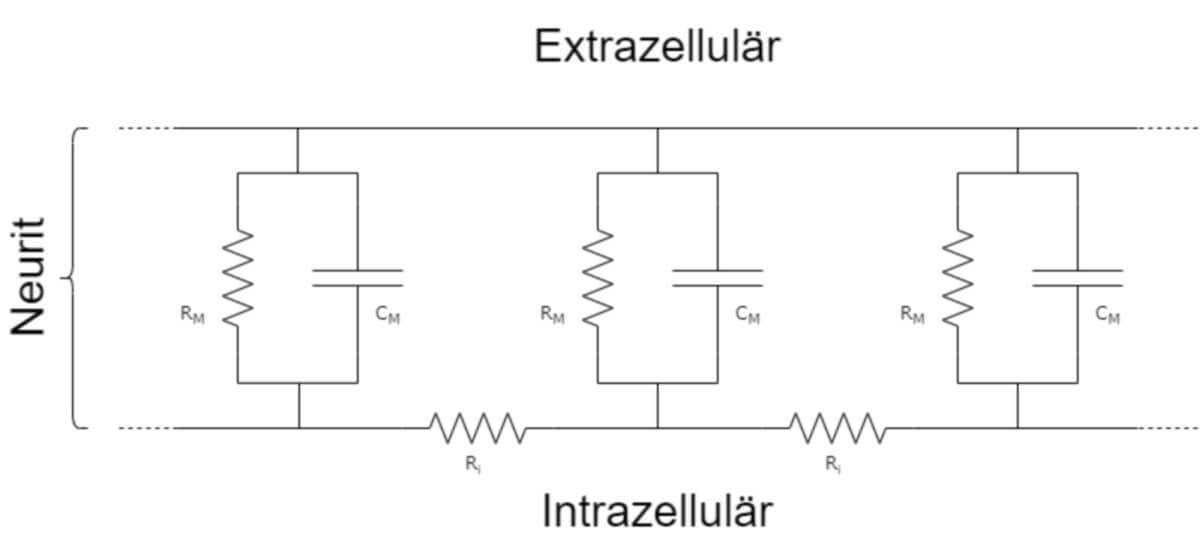
Zur Berechnung der passiven Erregungsleitung in Nervenzellfortsätzen werden diese vereinfacht als zylindrische Strukturen beschrieben, die aus in Reihe geschalteten Kondensator-Widerstand-Elementen bestehen. Die Elemente sind wiederum durch weitere Widerstände miteinander verbunden. Dabei entsprechen die Kondensatoren der Lipiddoppelschicht und die Widerstände der Elemente den in der Membran enthaltenen Leckkanälen. Die Widerstände zwischen den Elementen entsprechen dem intrazellulären Widerstand (R_i), der vom Zytoplasma gebildet wird. Die Spannungsänderung des Membranpotentials ist daher orts- und zeitabhängig. Außerdem nimmt die maximale Amplitude mit zunehmender Entfernung vom Entstehungsort des Signals (Reizes) ab.

Modell eines Neuriten nach der Kabel-Theorie

Aus dem Vergleich mit Kondensatoren und Widerständen lassen sich u.a. folgende Formeln ableiten. Die Spannungsänderung wird ortsabhängig mit einer Exponentialfunktion berechnet:

$${\displaystyle \Delta E_{max}(x)=\Delta E_{max}(0)e^{-x/\lambda }}$$

wobei:

• Längenkonstante (λ): berechnet aus Radius (a), Membranwiderstand (R_m) und intrazellulärem Widerstand (R_i)
• Ort (x)

Zur näherungsweisen Berechnung der Leitungsgeschwindigkeit passiver Nervenzellfortsätze wird folgende Formel verwendet:

$${\displaystyle v\approx {\frac {2\lambda }{\tau }}}$$

• Membranzeitkonstante (τ): Produkt von Membranwiderstand (R_m) und Membrankapazität (C_m)

Wenn R_m und R_i konstant sind, ist die Längenkonstante (λ) proportional zur Wurzel des Faserradius. Daraus kann die passive Leistungsgeschwindigkeit vereinfacht wie folgt berechnet werden:

$${\displaystyle v\sim {\sqrt {a}}}$$

Die mathematische Berechnung bezieht sich dabei jedoch auf passive Strukturen (z.B. einige Dendriten).

• Brandes et al. Physiologie des Menschen. Springer Link. 32. Auflage. S. 72-75. 2019