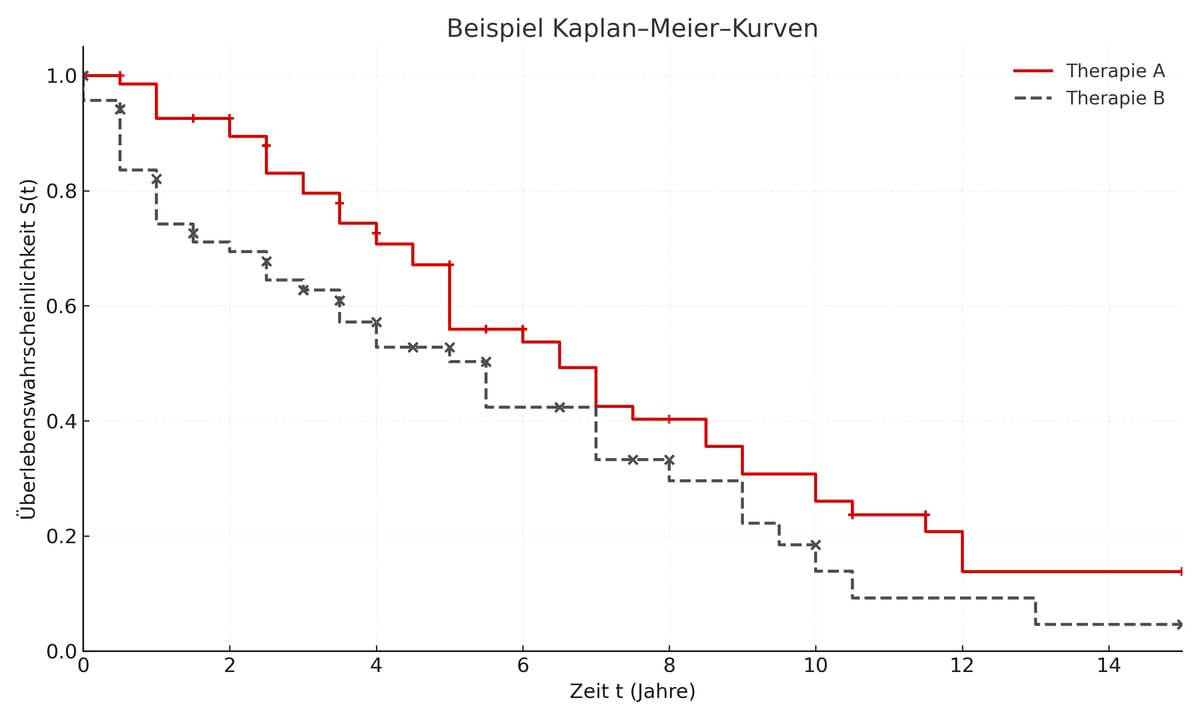
Kaplan-Meier-Kurve

Das graphische Ergebnis beruht direkt auf dem Kaplan-Meier-Verfahren. Für jeden Zeitpunkt, an dem mindestens ein Ereignis eintritt, wird die Überlebenswahrscheinlichkeit als Produkt der relativen Überlebenswahrscheinlichkeiten aller vorangehenden Ereigniszeitpunkte berechnet.

$${\displaystyle {\widehat {S}}(t)=\prod _{t_{i}\leq t}({n_{i}-d_{i} \over n_{i}})}$$

Dabei bezeichnet ${\displaystyle n_{i}}$​ die Anzahl der Personen im Risiko unmittelbar vor Zeitpunkt ${\displaystyle t_{i}}$​ und ${\displaystyle d_{i}}$​ die Anzahl der zu diesem Zeitpunkt eingetretenen Ereignisse.

Unvollständige bzw. zensierte Beobachtungen (z. B. Studienende ohne Ereignis, Verlust der Nachverfolgbarkeit) werden berücksichtigt, indem sie zwar die Anzahl der „im Risiko“ befindlichen Personen reduzieren, jedoch nicht in die Ereigniszählung eingehen. Die resultierende Schrittfunktion bildet das Überleben der Kohorte über die Zeit ab.

Beispiel

Beispielhafte Kaplan-Meier-Kurven zweier Kohorten im zeitlichen Verlauf

Eine valide Schätzung setzt voraus, dass Zensierungen „nicht-informativ“ sind, also kein systematisches Verhältnis zwischen dem Zeitpunkt der Zensierung und dem tatsächlichen Ereignisrisiko besteht. Ereignisse müssen eindeutig definiert und zeitlich korrekt erfasst sein. Bei niedrigen Fallzahlen oder wenigen Ereignissen steigen Varianz und Unsicherheit der Schätzung.

Die Lage und Form der Kurve erlauben eine visuelle Einschätzung des zeitlichen Auftretens von Ereignissen innerhalb einer oder mehrerer Gruppen. Unterschiede zwischen Gruppen werden standardmäßig mit dem Log-Rank-Test geprüft. Für eine adjustierte Analyse der Hazardraten wird meist das Cox-Proportional-Hazards-Modell herangezogen.

Kreuzende Kurven oder stark divergierende Hazardraten weisen auf zeitabhängige Effekte hin und erschweren die Interpretation im Sinne proportionaler Hazards.

Kaplan-Meier-Kurven werden in klinischen Studien zur Darstellung von Gesamtüberleben (OS), progressionsfreiem Überleben (PFS) und rezidivfreiem Überleben (RFS) eingesetzt. Darüber hinaus finden sie Anwendung in epidemiologischen Kohortenstudien, bei der Bewertung implantierbarer medizinischer Geräte oder generell bei der Analyse von Zeit-bis-Ereignis-Daten mit Zensierung.

Das Verfahren berücksichtigt konkurrierende Risiken nicht; Ereignisse anderer Art können die Schätzung beeinflussen, ohne dass dies in der Kurve sichtbar wird. Bei starker Zensierung, kleinen Fallzahlen oder frühen Ereignissen kann die Kurve instabil wirken. Außerdem erlaubt die Darstellung nur univariate Vergleiche; zur Adjustierung für Störfaktoren sind multivariate Modelle erforderlich.

• Kaplan, E. L., & Meier, P. (1958). Nonparametric Estimation from Incomplete Observations. Journal of the American Statistical Association, 53(282), 457–481.
• Kleinbaum, D. G., & Klein, M. (2012). Survival analysis: A self-learning text (3rd ed.). Springer.